|
|
|
 |
|
|
May
1991
AT&T Bell Labs 600 Mountain Ave.
Murray Hill N.J. 07974
Copyright © 1991 AT&T All Rights Reserved |
|
"The
Earth's Atmosphere looks like a convex lens. Why doesn't the sun
focus on the ground?" |
Your intuition that the earth's atmosphere
forms a lens which can focus light is correct, but fortunately it's
a weak lens and there is no danger of being fried like ants under
a magnifying glass.
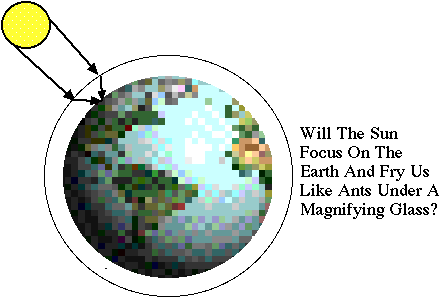
A glass sphere has a focal length which is
about the same size as the radius of the sphere (try a hand lens
or plastic globe to check). The focal length depends on the index
of refraction of the globe. If the earth were entirely made of very
clean water, the sun would nearly focus on the opposite side of
the planet. However, the index of refraction of air is smaller
than water by about their ratio in densities, which is about
a factor of 1000. Thus, the focal length of the "air
lens" formed by our atmosphere is about 1000 earth radii, or
a few million miles. Since the atmosphere is only a few hundred
miles thick, the focusing effect is hardly noticeable on the ground.
At sunrise or sunset when the sun is near the horizon,
there is a small flattening of the shape of the sun due to atmospheric
lensing. The lensing also shifts the apparent timing of the sunrise
and sunset by a minute or so, compared to an earth with no atmosphere. |
|
"
What is the Atomic Structure of a Noble Gas?"
|
(Note: This question was asked by a giggle of girls who
left a number and no name. It turned out to be Domino's Pizza.
Anyway, the question [as well as the pizza] wasn't bad, so..)
The six gases, helium, neon, argon, krypton, xenon and
radon, are referred to as "noble" gases because they are
chemically so inert. Noble gases comprise a very tiny fraction of
the atmosphere of Earth and are usually obtained by separating them
from air or from the gases released from subterranean sources such
as oil wells. That they had any reactivity at all was only
recently demonstrated in 1962 by N. Bartlett (who did much of his
work at Bell Labs)-when he isolated a red solid containing
xenon, platinum, and fluorine. As we shall see below, the
unique chemistry of the noble gases is particularly useful
in lasers and semiconductor fabrication technology.
In order to understand the atomic structure of a noble gas,
we must first lay a little groundwork for understanding atomic
structure in general. Atoms are composed of three basic particles:
electrons, protons, and neutrons. Electrically neutral atoms
have equal numbers of electrons and protons. This number is called
the "atomic number" and is the number that one sees
associated with each element in the periodic table of the
elements. It is the electrons that determine the chemistry of an
atom. For reasons rooted in quantum mechanics, electrons in
atoms group together into "orbital sets" (we'll
discuss quantum mechanics more fully in an upcoming newsletter).
These orbital sets have a number of special properties, one of which
is that they can contain up to a maximum number of electrons. Another
property is that these orbital sets have a ranking in energy. The
lowest energy orbital set is called the 1s ( pronounced "one-s"),
the next orbital set is called the 2s, which is followed by the
2p orbital set and so on. S orbital sets have the property
that they can hold only up to two electrons and p orbital sets can
hold up to six electrons. Incidentally, for those of you who
have already learned about orbitals, you may notice that the
p orbital set is made up of three individual p orbitals. Each
of these p orbitals contains a maximum of two electrons and
there are three p orbitals in the set, thus the total allowed
number of six electrons in the p orbital set. There are other orbital
sets, called d and f, which can hold up to ten and fourteen electrons,
respectively. So, if you look at your periodic table, one of the
noble gases is neon, designated by 10Ne. The "10" is its
atomic number so that we know immediately that neon has ten
electrons. How do we know which orbital sets these ten electrons
go into? The answer is that the electrons fill up orbital
sets to the maximum allowable number, starting with the lowest
energy orbital set first. The lowest energy orbital set is
the 1s which holds two electrons, the next lowest energy orbital
set is the 2s which holds another two electrons, then the
next lowest energy orbital set is the 2p which gets its full
measure of six electrons. Notice that for neon, all three
of these orbital sets are filled to the max. This is precisely why
neon is chemically so stable. You can think of chemical reactivity
as the quest for an atom to maximally fill its orbital sets. Atoms
without a completed shell of electrons try to steal electrons from
other atoms in a chemical reaction. Atomic neon starts out with
fully filled orbital sets and doesn't need to find more electrons.
In fact, we will need to pull out an electron from one of those
filled orbital sets to make neon react. This requires lots of added
energy which is why neon is usually chemically stable.
Noble
gases have a number of uses because they are chemically so stable.
For example, they are the gases which are put into fluorescent lamps.
Even passing an electric current through them in these lamps does
not cause them to react with any of the other materials in the glass
or fluorescent coating of the lamp. However, chemists have found
some conditions under which noble gases are chemically reactive.
Usually, these reactions involve the elements fluorine and chlorine
which are among the most highly reactive elements that we know.
( Incidentally, do not confuse fluorine with the fluoride in your
toothpaste-fluoride is an ionic form of fluorine which is chemically
much more stable. Likewise, the chlorine in a swimming pool is also
in a form which is chemically stable). An example of a compound
between a noble gas and fluorine is xenon difluoride (its chemical
compound symbol is XeF2) which forms colorless crystals at room
temperature. Xenon difluoride is highly unstable and will break
up into fluorine and xenon atoms upon heating. This makes it a useful
compound in semiconductor processing where fluorine is used to etch
silicon in the in the long process to make integrated circuit chips.
Fluorine is very reactive and the gas is hard to store and handle.
Xenon difluoride is more convenient to work with because it comes
as crystals that are somewhat less reactive. (Note that the term
"reactivity" for fluorine versus xenon difluoride is a
matter of degree-compare the reactivity of the wooden part of a
match in burning to the phosphorus/sulfur coated tip!). So,
during chip processing, xenon difluoride is put into a chamber with
the silicon, and heated to break it up into its constituent atoms
to start the reaction between the fluorine atoms and the silicon
wafer. For a more advanced treatise on the chemistry of noble gases
(which includes quite a bit of history), consult F. A. Cotton and
G. Wilkinson's classic treatise: "Advanced Inorganic Chemistry"
(Interscience Publishers, New York). |
|
"What
happens when an electron collides with another electron? " |
Before considering what happens when two electrons
collide, its worth considering a simpler, classical problem. What
happens when two bubbles in a glass of water collide?
As a bubble moves through the water, it pulls along some
of the adjacent liquid. When two bubbles are on a collision course,
they don't actually have to touch to scatter. Instead, the moving
fields of water around each bubble will first touch, deflecting
the bubbles from their path. The details depend on their relative
speed. When the bubbles move slowly they just bounce off each other.
At higher speeds they can hit, send off shock waves (sound) into
the liquid, and then continue slowly on their way. Some of the energy
from the collision might be turned into heat. This heat could boil
the water, creating new bubbles, which in turn scatter.
There are many similarities between electron and bubble collisions.
Electrons, unlike protons, neutrons or baseballs, are believed to
be "point particles", with a radius of zero, and thus
can never actually "hit". Like bubbles, however, electrons
drag a field around them as they move. This is their electric field,
originating from their electric charge. At low speed they simply
scatter off each other (like charges repel). The actual scattering
angles and velocities are determined by conservation of energy and
momentum. At slightly higher velocities they can collide and give
off light, instead of sound, as was the case with bubbles. Usually,
the light is in the form of two photons, going in opposite directions.
This makes it easier to conserve momentum. [We shake electrons back
and forth every day to generate "light". In a walkie-talkie,
electrons shake back and forth in the antenna. This produces radio
waves, which are made of photons of light which are at a wavelength
which cannot be seen. In a microwave oven, higher energy photons
capable of heating food are made in a device called a "klystron".
Shake electrons even faster, and you get visible light. Faster still,
you get X-rays like those at the dentist's office.]
At the highest energies new particles can be produced. By
Einstein's famous equation for the equivalence of mass and energy,
E=mc2 you'll need enormous energies (e.g. a room sized,
million volt accelerator ) to create enough mass to make a new particle.
You also can't start the collision with two electrons, and end up
with four, since this would violate conservation of charge. But,
with enough energy you can create pairs of electrons and their anti-particles,
positrons. Anything goes, providing you satisfy all conservation
laws, including conservation of energy, linear momentum, angular
momentum, and charge. |
|
I'm
making a bridge out of a paper tube. What is the stiffest tube with
the least weight? |
In a bridge, you are trying to maximize strength while reducing
cost. Thin tubes are used not so much to save weight, but as one
way to reduce the cost of materials. Since in most bridges the weight
of the road is transmitted by steel support cables to columns, we'll
concentrate on what makes a strong column.
There are two contributions to a column's strength. The first
is the intrinsic strength of the column material, and the second
is the way the material is arranged. Now, most building materials
are strong when squeezed ( known as compression) but not when pulled
(known as tension). For example, a plug of dried mud is hard to
compress, but easily breaks when pulled. Other materials are strong
when pulled, but not when pushed. For example, a steel wire is strong
in tension, but collapses when pushed. This is not because the material
is intrinsically weak in compression (after all, steel is pretty
tough) but simply because anything long and thin buckles sideways
when pushed sideways. Generally, materials are intrinsically stronger
in compression than in tension.
Compressional strengths can be very high. When you walk on
concrete, wood or metal floors no footprints are left behind. This
means the yield strength of flooring is greater than your weight
divided by the area your foot touches (about 150lbs/(2 in) 2~40
pounds/square inch [p.s.i]). However, a high heeled shoe can concentrate
all that weight in a 1/4 inch circle, for a pressure of 3000 psi,
enough to leave marks on a wooden floor. That's why high heeled
shoes and track cleats are kept out of the gym.
Still, walking on wood is not like walking on peanut butter; the
wood will dent until the air between the cell walls is compressed,
but your foot won't squeeze through to the next floor. Steel has
a yield point of about 200,000 psi, wood about 5000 psi, and paper
(which is really wood with no air pockets) somewhere in between.
So, if we want to make a wooden column to support 150 lbs all we
need is a rod about 1/8" in diameter (if you were building
a bridge, you might want to include a safety factor of two). However,
if we make a column one foot high and try to stand on the rod, the
slightest sideways force will cause it to buckle and collapse. What
can be done to make a column a foot tall, using no more wood than
the 1/8 inch rod?
The trick is to provide sideways support to stop the buckling
before it gets out of hand. One way is to tie some very fine strings
to the rod, and pull in the direction opposite the buckling. But,
this only begs the question since you still have to attach the strings
to some solid object. You could divide the 1/8 inch rod into three
1/16" rods (which have the equivalent volume) and connect them
with strings into a triangular tower. Strings will stop the rods
from bowing out by becoming taut, but won't stop the rods from bowing
in to the center of the tower. The best thing is to replace the
string with short wood rods, since short rods are stiff in tension
and compression.
You can try a simple experiment with a sheet of paper. The
paper is weak by itself, but folded in three and taped along one
edge it forms a triangular column. Place a book carefully on the
open top end of the column. Like the strings, if the edges try to
bow out the side walls become taut and prevent further bowing. If
the walls try to bow in, the walls are placed in compression. But,
any small sideways force (like your finger) or asymmetry in construction
will greatly reduce its strength. If we make the walls narrower,
they become stiffer (remember, a 1/8" rod is flexible only
because it is long; a 1/8'' cube is stiff). Thus, you might want
to use many tiny triangular columns glued together. Each one keeps
the walls narrow, and they all combine to prevent bowing. This structure
is, of course, nothing more than corrugated cardboard.
If you try to span a ditch with a tube, the strongest tube
for a given weight has the largest diameter. As you walk along the
tube, it bows down into the ditch. This places the top edge of the
tube under compression, and the bottom edge in tension. Providing
the tube doesn't buckle, the tube gets stronger by the square of
the radius (e.g. a two foot diameter tube is four times as stiff
as a one foot tube. To keep the weight constant, the wall thickness
is reduced accordingly). Internal supports to prevent buckling greatly
improve the strength of a tube bridge.
Nature values economy as much as bridge builders. Bundles
of thin walled tubes are used all the time to impart strength without
costing too much energy during growth. The structure of trees (which
use the hollow columns between cell walls to transport liquids as
well as stiffen), bee's honeycombs and insect exoskeletons are all
examples of nature's tendency to be efficient in the use of materials.
You might want to:
- Have
a contest to build the lightest, and strongest one foot cube pedestal
made of typewriting paper.
- Measure
the strength of tubes of different materials and wall thickness.
Try bamboo, tall grasses, wet or dry wood, wasp nests (we suggest
empty nests), plastic, .. Look for trends in the data. Good collaborative
project for a physics and biology class.
- Make
a (temporary) dam across a brook. Measure the yield strength of
wet and dry dirt, dirt with sticks mixed in, plastic, and so on
before you begin. Find out why beaver dams have one shape, and
the Hoover dam, another.
- Use
air to make a bridge out of weak material. Why is an air mattress
weak, but stiff when inflated with air (and air is about as soft
a material to strengthen a bridge as possible).
- There
is an old magic trick where you try to jam a paper straw through
an apple. Normally the straw folds up like an accordion. However,
if you put your thumb over the end when ramming the apple, it
goes through cleanly. Why?
|
|
Weightless
school bus |
Joanna Cole writes a wonderful series of science
adventure stories for children, involving Ms. Frazzle and
her magical
school bus. In her Lost in the Solar System story, the
children are launched into outer space. The question "Why do
people feel weightless in space?" is answered by "Gravity
gives objects weight. Without a large mass nearby, such as a planet,
there is no gravity to pull objects down, so they do not have weight".
A true statement, but incomplete. After all, the shuttle
astronauts are weightless, and they fly only 100 miles above the
earth. Why then are people weightless in space? |
|
What
are imaginary numbers and what are their uses? |
Imaginary numbers are not mythical creatures,
but are based on multiples of the square root of negative one, sqrt(-1),
which is simply written as i. The square root of any negative number
can be expressed as some multiple of sqrt(-1), e.g. sqrt(-9)=sqrt(9)*sqrt(-1)=3i.
Like the number "0", a placeholder for "nothing",
i took a long time to understand and find its place as a useful
mathematical tool. The need for i arises when you want a mathematical
operation on a number to generate numbers of the same kind.
For example, if we add any two integers we get another integer.
When an operation on a number generates only numbers of the
same kind, the operation is called "closed". Clearly,
most of life is concerned with "closed" operations; when
we add two sheep to three sheep we get five sheep, not a bunch of
cows. If we take the sqrt(3), we get a "real" number.
However, if we take the sqrt(-4), its clear the answer is not another
"real" number. Imaginary numbers were first used
by Renaissance mathematicians who also attached a great deal of
mystical significance to them. Leibniz, one of the inventors of
calculus, said, "The Divine Spirit found a sublime outlet in
that wonder of analysis, that portent of the ideal world,
that amphibian between being and not being, which we call the imaginary
root of negative unity." It was Gauss, around 1830, who really
understood imaginary numbers and how to use them.
Gauss understood that a new kind of complex number could
be written, and this number would contain a real part and an imaginary
part. Typical complex numbers might be 5+3i or a+bi, where 5 or
"a" are the real parts and 3i or bi are the imaginary
parts. Gauss showed that these numbers could be added, (a+bi )+
(c+di )= (a+c)+(b+d)i , or multiplied, (a+bi)* (c+di )= a*c+a*di+c*bi+d*b*i2
and since i 2= sqrt(-1)2=-1, the whole expression equals (ac-bd)+(ad+cb)i.
Once mathematicians understood these concepts, a whole new
area of mathematics was open to study. Even relatively simple
ideas, like prime numbers, changed. The prime number 2 can be factored
as (1+i )*(1-i ), 5 as (2+i )*(2-i ), and 29 as (5+2i )*(5-2i ),
but 7, 11, and 19 cannot be factored. Surprisingly, Gauss found
that many ideas in number theory are easier to solve using complex,
rather than real numbers, as originally posed.
One interesting and suggestive use for complex numbers
comes from repeatedly multiplying i. by itself.
|
i*i=
-1 |
left
|
|
i
*i*i = -i |
down
|
|
i
*i *i *i = 1
|
right
|
|
i
*i *i *i*i = i
|
up
|
|
i
*i *i *i*i*i= -1
|
left
|
|
Note how the sequence repeats itself after four iterations.
This, so to speak, means you're going in circles. We can think of
a multiplication by i as a rotation of 90 degrees. By labeling the
x axis by the real part of the complex number, and the y axis with
the imaginary part, complex numbers can be represented by arrows
in the plane. The number 3+2i can be placed on this coordinate system
by going three steps along the (real) x-axis and two steps
parallel to the (imaginary) y-axis. Rotating this vector by 90 degrees
means multiplying 3+2i by i =3i -2 (See drawing. It really works).
This idea of arrows rotating around the origin is very useful--recurring
phenomena like alternating electrical currents, pendulums, the wave
nature of light, are all often represented using complex numbers.
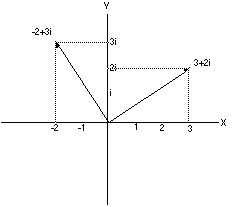 |
Two
complex numbers can be added by placing the tail of the arrow
representing the second complex number at the head of the first
arrow (you are not allowed to rotate the second arrow). The sum
is the new arrow drawn from the origin of the coordinate system
to the head of the second arrow. If we add 1+2i to 3+2i we first
place the arrow for 3+2i as above. Now, from the head of the
arrow go one more step parallel to the real -axis and two
steps parallel to the imaginary y-axis. You (or your pencil) are
now standing4+4i steps from the origin.
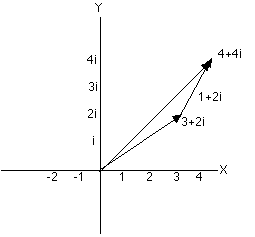 |
Complex
numbers, since they can be represented by a that have both length
and direction, are used to represent many physical quantities. (Note:
Gamow has a great story about using complex numbers to find
buried treasure on a desert island in his book One Two Three...
Infinity ( George Gamow, Bantam Books, New York 1967). There is
more about complex numbers (and their applications) in the books
Asimov on Numbers by Isaac Asimov (Pocket Books, New York, 1977),
and Gauss by Ian Stewart in Scientific American, July 1977.)
|
|
Myth
of the Month: |
At the Spring Equinox a number of classes tried to balance
an egg on its pointy end. Supposedly, the alignment of the earth's
axis and the sun in some way help "balance" the egg. Although
you can get an egg to balance at any time of year by sprinkling
some salt on the table for it to rest on, or by using an egg with
a rough surface texture, the stars have nothing to do with the egg's
propensity to fall. As it turns out, the gravitational pull of your
stomach on the egg is about one billion times more critical than
the sun in determining if the egg will fall left or right (Hint:
just calculate the difference in forces across the egg due to the
sun or your body. It is the difference in forces across the egg
which help orient top and bottom.) |
|
NOTE:
THIS ADDRESS AND PHONE NUMBER IS NO LONGER ACTIVE! (as of 1993)
|
If you have any comments on this newsletter, call
1-800-CLEARUP or write
- CLEARUP
c/o AT&T Bell Labs
600 Mountain Ave.
P.O. Box 636
Murray Hill, N.J. 07974
|
|
|