| g e n u i n e i d e a s | ||||||
 |
 |
 |
 |
 |
 |
 |
| home | art and science |
writings | biography | food | inventions | search |
| eureka brines |
|
November 2011 Over 2000 years ago Archimedes discovered the law of displaced volume while taking a bath. According to an apocryphal story, he was trying to figure out if a gold crown belonging to King Hiero of Syracuse had been adulterated with silver. Gold is denser (and more expensive) than silver, so a pure gold crown weighs more than an identical crown diluted with silver. And its cheaper too, so the jeweler risked death if caught defrauding the king. But Archimedes did not have access to an identical crown. If he knew the volume of the crown, and its weight, he could easily calculate the resulting density, and see if it matched pure gold- but how to measure the volume of an ornate headpiece? The answer turned out to be very simple. When Archimedes stepped into his bath, he noticed the water level rose, and realized the volume of displaced water was equal to the volume of his submerged body. Crying EUREKA ("I have found it" in ancient Greek) he ran excitedly down the street naked- proclaiming not only the law of displaced volume, but reinforcing a millenia-old caricature of the absent minded professor. Why is Archimedes's discovery relevant to salt brining? Well, we may not own an ornate crown like Hiero, but salt particles are even more beautiful and complex than wrought gold under a microscope. These photos of three different kinds of salt illustrate their variety, running from flaky to cubic to granular. Every brand is slightly different, even if they are sold under the same name:
The ratio of salt to air depends on how tightly these oddly shaped particles can be packed1. If you measure out a "cup" of salt, each brand might differ in weight by more than a factor of two! Pretty important if a recipe calls for "one tablespoon of salt"- dinner might be over salted with fine sea particles, and under salted with Kosher flakes. Of course, if recipes used weight instead of volume measures, there wouldn't be a problem. One ounce of salt is one ounce of salt atoms, no matter how many tablespoons it takes to measure out that ounce. Unfortunately, too few people own accurate kitchen scales. But there is a solution based on Archimedes's insight. To understand the method, we don't even have to go into the kitchen- just perform what scientists call a Gedankenexperiment (German for "thought experiment"). Imagine you want to brine a Thanksgiving Turkey (click here for more on the effectiveness of salt brines). I suggest the following method to formulate a gallon of brine:
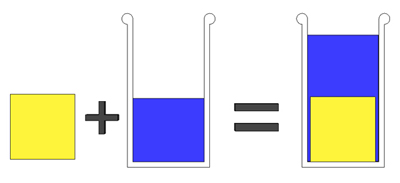
Why does this method work? Imagine you have one cup of dry salt. Now, slowly dribble in water until the liquid level is just at the original salt level of one cup. If you poured in a third of a cup of water, then 2/3rds of the volume of dry salt was air. And if you know the density of solid salt, and its volume, you know its weight. Just like the King's crown. Microscopically, consider a solid block of pure salt (yellow cube) which occupies exactly one cup in volume. And you place it in a flask containing one cup of water. By Archimedes's Law, the water will be displaced and the water will rise to the "2 cup" level:
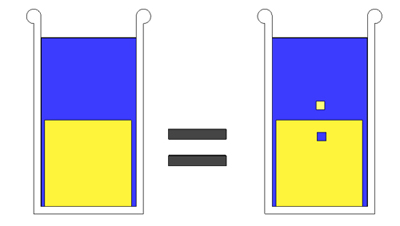
Now imagine removing a little piece of salt from the block, and placing it in the water, and filling the hole with water. Has the level changed? Of course not. If we put 1 cc of salt in the water, it displaces 1 cc of water, which exactly fits back into the 1 cc hole. So the level doesn't rise:
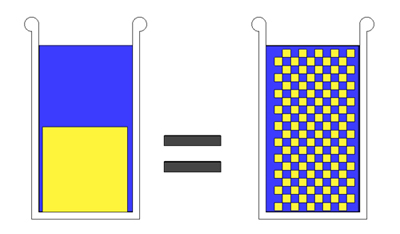
Now repeat this experiment over and over, grinding up the salt cube. If we grind into large flakes like Kosher salt, there are large gaps between each crystal. But large or small, no matter what the shape or the density, the water level is unaffected:
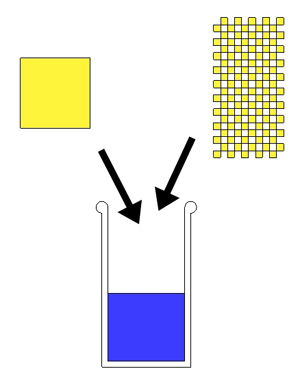
So here is the answer. If we mix in a solid cube of salt, or the equivalent weight of salt in any shape or size, the water will always rise to the same level. Working in reverse (if we don't have a scale), we just pour in salt until the target level is reached. Sometime it might take a cup of salt, sometimes two- but it will always incorporate the same weight of salt after displacing the same volume of water.
The perfect brine, every time. Besides brining, a related discovery by Archimedes-(his principle of buoyancy) is the science behind a Cartesian diver toy that is powered by a desk lamp.
|
|
-------------------------------------------------------------------------------------------------------- Additional articles on kitchen science can be found HERE.
1There is an entire field of mathematics called "packing theory" dedicated to calculating how tightly different shaped objects can fit together. In two, three and even more dimensions. Packing theory is not only beautiful, but has many practical applications in manufacturing, biology and even code breaking. 2In this recipe, salt is added to a gallon of water (plus the one cup of hot water). Salt is 2.165 times as dense as water. So, the added salt has the same weight as the 4 oz of water it displaces times its density, or 8.66 oz. Thus the percentage salt, on a weight basis, is 8.66 oz/(one gallon + one cup+ 8.66)= 8.66/(128+8+8.66)~6%. How much salt ends up in the meat depends on how long you brine, how much salt is exuded with the cooking juices, etc. Realistically, any mixture around this level is fine- don't sweat the measurements. Scientists cringe at the use of the same units for volume and weight- e.g. ounces, because at best its true for only one material with one specific density at one temperature. Its almost exactly true for water- one volume ("fluid") ounce of water actual weighs 1.04 ozs (surprising, since water density at room temperature is actually LESS than one), and in the kitchen its ok to treat water weight and volume as identical. But a cup of salt does not weigh 8 oz, and a cup of oil only weighs around 7 oz. Which is why accurate recipes have abandoned the use of volume measures, and moved entirely to weights. For the specialist, there is also a VERY tiny correction to this method arising from the volume shrinkage of salt dissolved in water. Just as a bit of air intrudes between the grains in a salt shaker, there is a bit more space between the sodium and chlorine ions in crystalline salt compared to their ability to crowd into the nooks and crannies of liquid water. So if you dissolve 1 cc of solid salt into a large volume of water, the water will only rise by 0.985cc. In a saturated solution like the initial brine above, the effect is even smaller because the nooks and crannies fill up quickly. I doubt this phenomena would proportionately reduce the salt concentration by 1%, i.e. to 5.94%. Well under your ability to measure out the ingredients. But still interesting. CHANGES IN VOLUME UPON SOLUTION IN WATER OF THE HALOGEN SALTS OF THE ALKALI METALS. II., Gregory Paul Baxter, Curtis Clayton Wallace, J. Am. Chem. Soc., 1916, 38 (1), pp 70–105, January 1916
|
 Contact Greg Blonder by email here - Modified Genuine Ideas, LLC. |