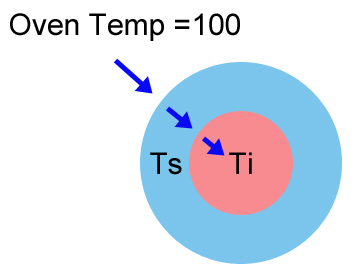
When you cook a piece of meat in an oven or a smoker, the meat's interior temperature naturally rises over time. However, the detailed change in temperature as a function of time is the result of many complex, interacting effects. Convection and conduction bring warmth from the surrounding air deep into the mass of protein and fat. Water is released, evaporatively cooling the meat's surface. Enzymes break down proteins and collagen, swelling muscle bundles, forcing out more liquid. Mass is lost, heat capacities morph.

In order to separate out these effects (particularly those leading to the well-known barbecue "stall"), it is useful to establish a baseline- how fast would a solid sphere of similar mass, thermal conductivity and heat capacity warm, without the complexities of chemistry or latent heat considerations?

An accurate model is too complex to build intuition- even our simple faux-meat sphere's temperature rise depends on a detailed knowledge of convection currents, boundary layers and oven temperature gradients. But, we can get 90% of the way there with a simple model based on Newton's Cooling Law.

Newton hypothesized if two objects of different temperatures were connected, the cooling (or heating) rate would depend linearly on the difference in temperature between the two objects. This law is roughly applicable in a wide range of circumstances.

I've adapted the Newton Cooling Law to a sphere. If you assume the interior of the sphere is highly thermally conductive and at one temperature, the sphere heats quicker than reality. That's because meat is modestly insulative, slowing down the transfer of heat from the oven to the interior. So I added a second, inner layer to the sphere, to phenomenologically allow for this delay. The oven air heats the surface layer, which then heats the inner layer, following Newton's Cooling Law.

In this model, Ts is the surface layer temperature, and Ti the interior core temperature (both initially =0). Each layer has a characteristic time constant that determines how fast heat flows from the exterior. Small time constants lead to rapid conduction.

Amazingly, this simple model fits actual cooking data pretty closely! Try varying the thermal time constants of the outer (blue) and inner (pink) layers, and compare to the curves on the barbecue "stall" page (e.g. double click on the blue or pink boxes to modify the time constant). It captures the essence of the sand bath, the fat log, and the initial and final slopes of the meat curve (before and after evaporative cooling plays a role).

(javascript renovation in progress)

--------------------------------------------------------------------------------------------------------

Additional articles on kitchen science can be found HERE.
  Or follow me on twitter for (very occasional) alerts of new food science postings at @KitSci
In the practice of all-things barbecue, we appreciate the support and conversations with Meathead at AmazingRibs.com, Sterling at BigPoppaSmokers, along with numerous competition pitmasters and backyard chefs.